数学がわかると世界がわかる。
論理的思考力、
課題発見解決力が高まっていく。
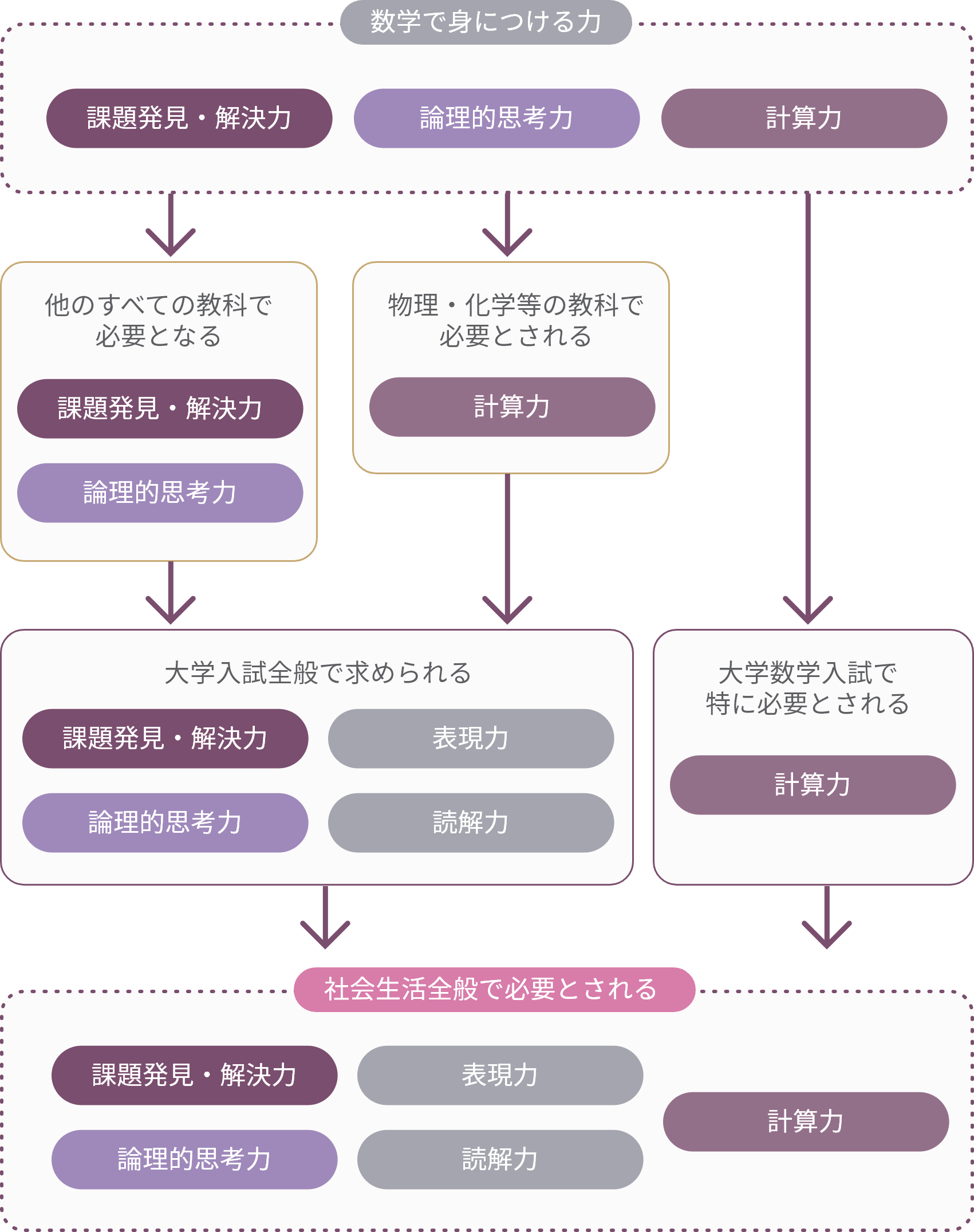
計算力を身につけるのはもちろん、
理科(自然科学)の理解の基礎となり、
論理的思考力や課題発見解決力をみがくのが数学です。
大学受験科目として選択する生徒に合格できる実力を
つけていくことはもちろん、選択しない生徒にも大学での
学びや社会人としての将来に不可欠な力を育成しています。

ICTを活用したわかりやすい授業
大妻嵐山ではタブレットPCを全生徒が持ち、教室には電子黒板が設置されています。数学の授業でも抽象的な概念をビジュアル化したり、グラフを動かしたりすることで、生徒のより深い理解を促しています。

グループ―ワークで難しい問題もみんなで協力して解く
自分が人に教えたことは忘れない。このセオリーを適応して、教え合い・学び合いのアクティブラーニングを数学の授業でも頻繁におこなっています。先にわかった生徒がまだの生徒に教えるグループワークで、先生一人だけが教える授業よりも理解しやすくなります。

放課後の質問タイムで「わからないまま」をなくす取り組み
数学は、ある単元をわからないままにしておくと、そこから先がますますわからなくなる積み上げ型の教科です。だから、「わからないまま」をなくすために、放課後の職員室や廊下はいつも先生に質問に来る生徒たちでにぎわっています。
数学検定を中学3年以上はほぼ全員受験して3級以上に合格
大妻嵐山では数学の理解力をより確かなものにするために、数学検定を中学3年が受検し、中学3年のベンチマークとされている3級以上にほぼ全員が合格しています。

学校を飛び出し数学甲子園にチャレンジ
数学の得意な生徒が3~5人1チームになって、毎年、数学甲子園にチャレンジしています。まだまだ大きな成績は残せていませんが、一歩踏み出しチャレンジすることで生徒たちは成長していきます。
数学は計算力を養成する教科であり、
物理や化学、生物などの理科(自然科学)の理解に不可欠です。
大学受験で数学を選択しない生徒も少なくありませんが、大学での学びや社会人としての活動に不可欠な論理的思考力や課題発見・解決力を高める重要な教科です。
大妻嵐山では、「探究心の養成」「課題発見・課題発見解決力の育成」「論理的思考力の育成」等を卒業までの目標にして、まず中学1年では、「興味・関心」を養いつつ、基礎力と計算力をきたえます。
そして、中学2年では「知識・理解」の深化を、中学3年では「自主的探究」を目標にして高校でのより高度な数学の学習に移行準備を進めます。
高校1年では「課題発見」を目標にしてさまざまな事象を数学的に考える力を育成し、高校2年では大学受験を意識して「思考力・応用力」の強化に取り組み、さらに高校3年では大学受験に合格できる数学の実力を育成していきます。
このプロセスに一貫しているのが、アニメーションなどを使って二次関数なども視覚的に理解できるICT(タブレットPCや電子黒板などの情報通信技術)の活用、そしてアクティブラーニングです。数学が苦手な生徒も、難しい問題をグループで協力しながら解くことによって、数学がわかる楽しさを感じつつ学んでいきます。
| 中1 | 中2 | 中3 | |
|---|---|---|---|
| 目標 | 興味・関心の養成 基礎力・計算力の強化 |
知識・理解を深める | 自主的探究 |
| 高校数学を学ぶための基礎を確立し移行を準備 | |||
| 育成の方策 | アクティブラーニングやICT活用により 「思考力・判断力・表現力」「主体性・協働性・多様性」を育成 |
||
| 副教材・小テスト・計算プリントの活用により「知識・技能」の定着 | |||
| 検証(目標) | 数学検定5級 | 数学検定4級 | 数学検定3級 |
| 高1 | 高2 | 高3 | |
|---|---|---|---|
| 目標 | 4技能獲得 グローバルマインド獲得 |
4技能獲得 グローバルマインド獲得 |
グローバルを視野に 進路選択 |
| 育成の方策 | アクティブラーニングやICT活用により 「思考力・判断力・表現力」「主体性・協働性・多様性」を育成 |
||
| 副教材・小テスト・計算プリントの活用により「知識・技能」の定着 | |||
| 検証(目標) | 数学検定準2級 | 数学検定2級 | 数学検定準1級 |
| 数学甲子園 | |||
単に問題を解くのではなく
考えることを楽しみましょう
数学の解き方を言葉にできることの大切さに気づき、
言語技術指導の研修を受けて
数学授業に取り入れていれています。
それにとどまらず、中学生の
「言語技術」の授業も担当するほど、
言葉からのアプローチを重視しています。
「やればできるかも」と感じれば数学は苦手ではなくなる
女子だから、数学はできないという意識を持つ生徒もいますが、そんな苦手意識を捨てて「やればできるかも!」という気持ちが持てるような授業を心がけています。
数学の授業を通じて、生徒には「論理的に考える力」「機械的に数字を処理する力」「根気強く問題に向かい合う力」を身につけてほしいと願っています。
なぜそう解いたのかを言葉にすることの大切さ
ですから、授業では「どんな風に考えたらよいのかを問題の条件から考え、自分たちが知っている知識をフルに活用して解いてみる」という過程を大切にしています。どうしてその様に考えることができたのかを、直観ではなく論理的に説明できるようになると、その問題を本当に理解して解けたということになるからです。
例えば図形の問題で「この2つの直線、平行のような気がする!」と直感で気づいた生徒がいたとします。そんなときには「どうして平行になるのか言葉で説明してみて!」と問いかけると、周りの生徒と一緒に一生懸命理由を言葉にしています。このように、場合によってはグループで議論し、お互いに考えや解き方を深められるように心がけています。
また、中学生では、問題の意味がわかりづらいということもあります。そんなときには、できるだけ具体例を挙げて説明するようにしています。数学に入る手前でつまずかないようにするためです。
「わからなかったことが、わかるようになる」面白さを知ってほしい

数学的なセンスや基礎力を身につけると大好きな音楽がもっと楽しめるようになる。
何の先生になろうかと迷ったときに、そう考えて数学の先生になる道を選び、数学はあらゆることの基礎だと生徒に熱く伝えています。
「わかる!」を大切にした授業を心がけています
人工知能(AI)が影響を持つ社会が来ようとしていますが、そんな社会でも必要とされる「問題解決能力」「コミュニケーション能力」「洞察力」は、数学の授業展開の中で養うことができると思っています。
私は生徒には「学ぶ楽しさ」を知ってほしいといつも考えながら授業をしています。数学というと、難しい科目と思う生徒も多いのですが、でも、どんなことでも自分がわからなかったことがわかるようになるのは、本来は楽しいことのはずです。知らなかったことを新たに知ることも素晴らしい経験です。
だから、生徒の「わかる!」を大切にし、そう感じられる授業を目指して、常に生徒の状況を確認しながら、熟練度に合わせた授業をしています。
協力して解決するのも数学の面白さです
そして生徒には、見通しを持って筋道だてたものの考え方、課題解決にチームで取り組む力、自分の考えを表現する力を身につけてほしいと、思っています。
特に数学は、一人で黙々と問題を解く科目だと思われがちですが、協力して解決したり、教えたり教わったりすることで、深い学びへとつながっていきます。もちろん一人で静かに机に向かって考えることも大切ですが、「ああでもない」「こうでもない」と周りと話をしながら解くことができたとき、一人で解けたときとはまた違った達成感を味わうことができると思っています。
ですから、授業ではこの時間の内容の解説・例題を個人で考える⇒グループで相談しながら解決する(=アクティブラーニング)⇒ふりかえりと解説という流れが中心になっています。またアクティブラーニングを取り入れることで、自分と生徒と一緒に授業を組み立てていく楽しさを感じています。













